Физики научились искать объекты в сыпучей среде. С помощью ультразвука и теории случайных матриц

Австрийские и французские физики разработали метод обнаружения тел, скрытых в толстом слое гранулированных сред и суспензий, с помощью теории случайных матриц и отпечатка искомого объекта. Разработанную математическую модель ученые проверили в трех экспериментах, доказав ее высокую точность (в одном из опытов вероятность ложного детектирования составила менее 10-8), а также предложили использовать модель в медицине для диагностики нервно-мышечных заболеваний. Результаты исследования опубликованы в журнале Nature.

Чтобы заглянуть в толщу некоторой неупорядоченной среды, например, слоя сыпучего материала, физики используют многоэлементные устройства — массивы детекторов, которые фиксируют прошедший или отраженный сигнал. А поскольку неоднородные среды можно рассматривать как реализацию случайных процессов, исследователям также помогает теория случайных матриц. Все это позволило ученым визуализировать объекты, скрытые под слоем пористого или зернистого вещества: в оптике для этого применили методы формирования волнового фронта, а для акустики приспособили зеркала, обращающие время.

Однако в более сложных случаях эти подходы неприменимы, так как в общем виде невозможно проверить однозначное соответствие между каждым собственным состоянием матрицы и каждой целью в материале. Особенно если помещенные в сыпучую среду цели не слишком хорошо отражают сигнал, а окружающая среда достаточно хаотична. Другими словами, в режиме сильного многократного рассеяния не получается полностью скомпенсировать влияние беспорядка.

Физики из Австрии и Франции под руководством Александра Обри (Alexandre Aubry) из Высшей школы промышленной физики и химии решили эту проблему, предложив искать корреляции в рассеянных волнах вместо нивелирования хаотичности в толстом сыпучем веществе. Для этого ученые построили инвариантный оператор из матрицы пропускания в неупорядоченной среде и сопряженной транспонированной матрицы для однородной эталонной среды: чтобы найти объект внутри материала, достаточно подействовать таким оператором на предполагаемый отпечаток предмета. Исследователи доказали, что собственные состояния предложенного преобразования это моды, которые не изменились после рассеяния и продемонстрировали картину прошедшего поля за изучаемой средой. Эта картина в свою очередь оказалась идентичной картине чисто баллистических волн, независимо от числа актов переизлучения и отражения.

Свою математическую модель физики подтвердили с помощью трех экспериментов. Первый заключался в ультразвуковой визуализации двух металлических сфер размером 10 и 8 миллиметров, помещенных в гранулированную суспензию из воды и стеклянных шариков диаметром 300-315 микрометров. Поверх среды авторы работы поместили двумерный массив из 1024 детекторов, который зафиксировал оба объекта с высокой достоверностью (вероятность ложного срабатывания составила 10-8), но сильным эхо-сигналом. В дополнение к этому опыту физики изучили, как изменился инвариантный оператор в случае, когда одна из сфер тонула в суспензии — ученые с хорошей точностью отследили траекторию объекта.

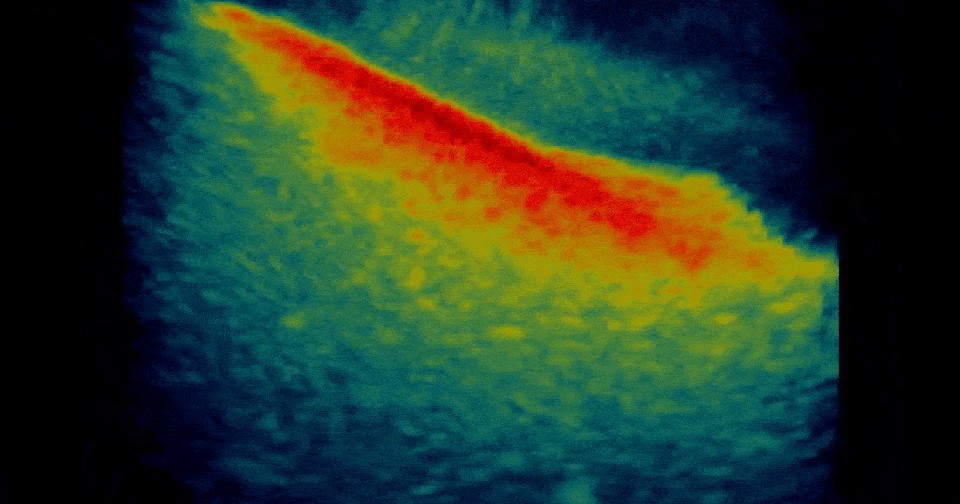
Во втором эксперименте исследователи использовали маркер повреждения, который обычно применяют для мониторинга опухолей молочной железы в клинических условиях. Этот маркер ученые поместили в воду, а затем подсчитали ультразвуковой спекл, сгенерированный водной пеной. Наконец, третьим экспериментом стало картирование локальной анизотропии волокнистой среды: физики визуализировали мышечную ткань с помощью решетки из 256 ультразвуковых преобразователей, сработавших в диапазоне частот 5,5-9,5 мегагерц. Результат позволил ученым практически полностью определить пространственные характеристики каждой мышцы.

Авторы новой методики отметили, что второй и третий эксперимент в будущем могут стать крайне полезными для медицинского применения. Например, результаты последнего опыта можно использовать для наблюдения нервно-мышечных заболеваний, а также нарушений миокардиальных волокон, которые возникают на ранних стадиях кардиомиопатии и фиброза.

О том, как теория случайных матриц помогла описать упорядочивание жидких кристаллов, мы писали ранее.

Источник